Turbulence Noise
By Neil Blevins
Created On: May 6th 2015
Updated On: Dec 7th 2024
Software: 3dsmax, Filterforge
In this tutorial I hope to teach you a little bit more about
Turbulence
Noise. Many apps including 3dsmax have various noise types, and
frequently you'll find regular noise, fractal noise, and Turbulence
noise. In an earlier article, I discussed Fractal Noise in great
detail, showing how it can be constructed using layered copies of
regular noise, so now this article will do the same with Turbulence
Noise.
Perlin Noise in 3dsmax
So for this example, I will again be using Perlin Noise, although the
Turbulence "formula" can really be applied to any noise type (you'll
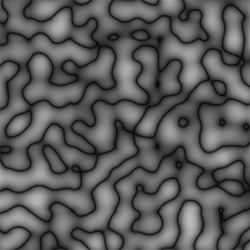
see an example of this later). Here's an example of Perlin Noise,
this is the 3dsmax "Noise" Map, set to regular, which is simply perlin
noise...

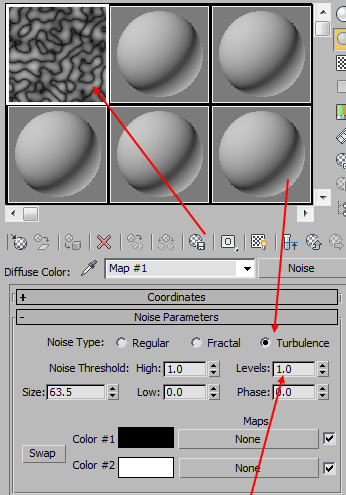
Perlin Noise with Turbulence in 3dsmax
Anyone who has used 3dsmax knows that to get
Turbulence noise, you can just take your Noise Map and click the
"Turbulence"
radio button...
But how does Turbulence
actually work under the hood?
So Turbulence is actually quite simple. Take your Perlin Noise, and
take the absolute value of it. For those who need a math refresher,
absolute value means to get rid of the minus sign. So a value of 1
becomes 1, a value of 2 becomes 2, a value of -1 becomes 1, a value of
-10 becomes 10. Its the distance to the value from 0.
So lets say we wanted to construct Turbulence using 3dsmax from a
regular noise, much in the same way as we did Fractal Noise in the
previous lesson. There are a few issues standing in our way. First,
regular noise in 3dsmax goes from a value of 0 to 1, or black to white.
To get this formula to work, we need our noise to go from values of -1
to 1. And second, there is no absolute value function in 3dsmax. So
we'll have to construct our own.
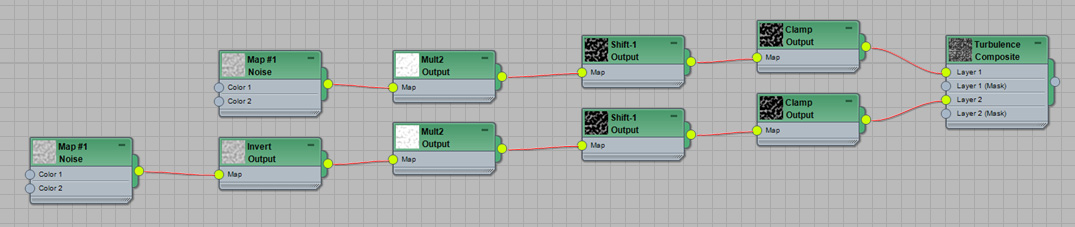
Here's the network of nodes to construct Turbulence...
And here's a 3dsmax file that shows how it works, Max 2011 version: Turbulence.zip
So here's a quick run-through of the network. I am taking two identical
noises set to regular. I invert one of the noise's colors. I then
multiple both by 2, which means my noises no longer go from values of 0
to 1, but go from values of 0 to 2. I then shift the values by -1. So
now both noises go from -1 to 1. I then clamp both noises, which means
I now have the first noise which contained the values from -1 to 0 now
go from 0 to 1, and the second noise which contained the values of 0 to
1 go from 0 to 1. And then I add the two noises together using the
Composite Map.
The result is two identical noises, the first image below is using the
turbulence mode
of 3dsmax's Noise Map, and the second image is our hand made Turbulence
Noise using
perlin noise.

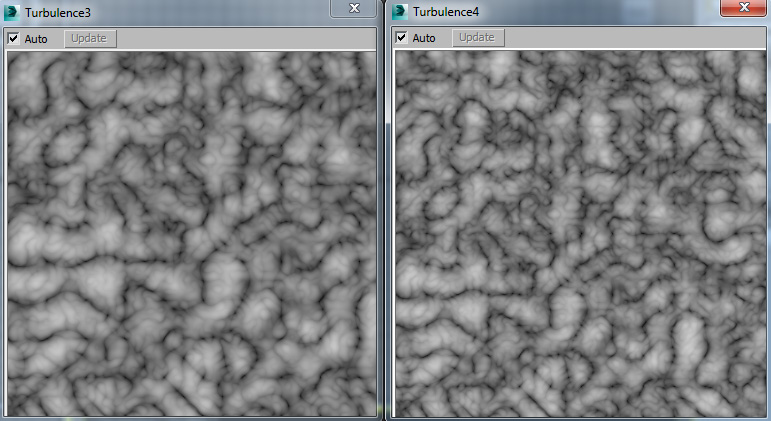
Now, what if we want turbulence with several fractal iterations? Well,
this is a little more complex. You'll remember from the Fractal Noise lesson
that what you have to do is mix multiple noises at different sizes and
intensities. This can be done with turbulence too. So in the first
image below is a single Noise Map set to turbulence, and levels
(iterations) set to 3. The Second Image is our handmade turbulence
where we use the same technique we discussed in the Fractal Noise lesson,
layering the noise iterations together using Composite Maps.
Of course, the network for the hand constructed Turbulence with fractal
iterations is super ugly, since I'm mixing 3 different iterations
together...
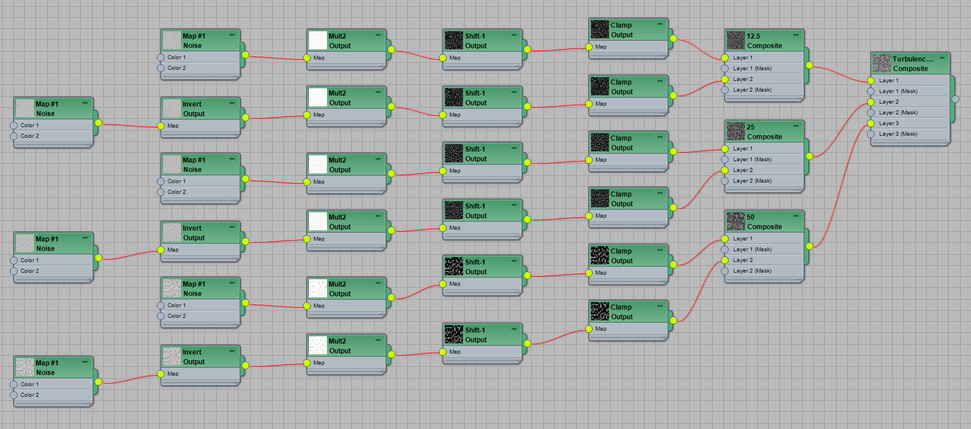
Now that we know all the details, lets look at a way to do the same
thing that's a lot cleaner. Instead of doing all of the math using
nodes to get our absolute value, you can also apply a Color Curve to
the noise. Check this out...
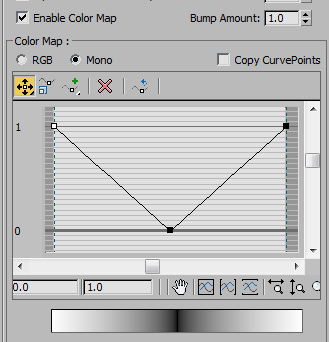
This will take all values between 0 and .5 and invert them, and takes
all values between 0.5 and 1 and maps them from 0 to 1. The result is
the same as the multiple nodes above. Do note though, you still have to
make your fractal manually. Here's the new simpler network...
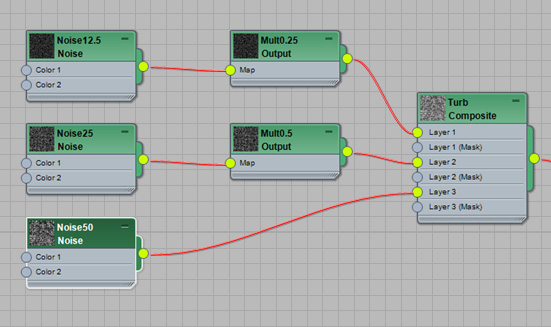
Of course, now the obvious question, why on earth would you want to do
this? Well, in the case of 3dsmax and perlin noise, the answer is you
don't. I highly recommend just using the turbulence radio button in
regular noise to get this effect. But constructing it manually has 2
advantages.
- First, its just good to have a better understanding of the math
behind what's going on. Something similar to this network is exactly
what's happening in the code inside the regular Noise map set to
turbulence.
- Second, if your favorite 3d app like Blender doesn't have
Turbulence, you could construct it by hand.
- And third, you can now use this knowledge to make a turbulence
of any noise you want. As an example, The Bercon Noises,
a plugin for 3dsmax, has the ability to use turbulence with Cellular
Noise. Here's an example...
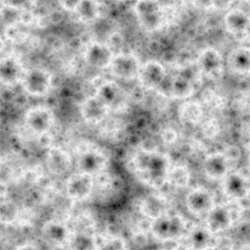
Now lets say Bercon Maps doesn't get recompiled for your copy of
3dsmax, and you really need this noise. No problem. Just do exactly
what I did above, but instead of using the Regular Noise maps as your
base noise, use a Cellular map. This recipe works for any base noise
type, so you can add turbulence to any noise you want.
Perlin Noise with Turbulence in Filter Forge
Filter Forge is a
powerful pattern generation program. However, I noticed it didn't have
any turbulence noise type. So, since I know the math behind it, I
constructed my own...
Here's the original Perlin Noise in Filter Forge...

And here's what it looks like after I did turbulence with 3
iterations...

Notice that this pattern looks slightly different from the 3dsmax
Turbulence. That is simply because 3dsmax and Filter Forge use a
slightly different type of Perlin Noise.
And here's the network that created the Filter Forge Turbulence which
uses an absolute value node...

But Filterforge allows you to do even a cleaner version. All Noises
have a parameter called Profile. And you can pump an Impulse node into
the profile, which contains a similar curve to the Color Map I used in
3dsmax...
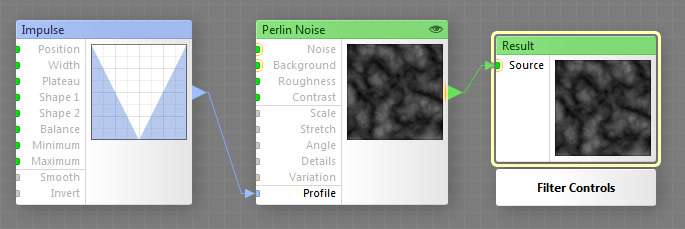
What's better is the profile is applied BEFORE the fractal iterations,
whereas the max Color Map is applied AFTER the fractal iterations. So
in Filter Forge, you don't need to manually add the fractal iterations
in your graph, you can just use the fractal iterations inside the
Perlin Noise node, which avoids a whole lot of extra nodes in your
graph.
Of course another nice thing about Filter Forge is you can group nodes
together, making it appear even simpler...
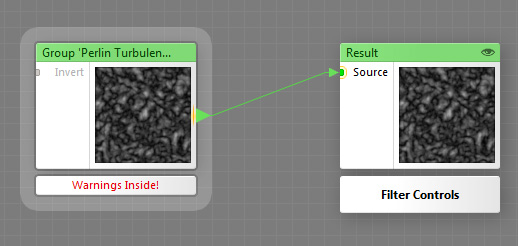
Hopefully this gives you just a little more insight into how Turbulence
noise works, and gives you the ability to manually add Turbulence to
any noise type or procedural noise generation program that may need it.
This site is ©2025 by Neil Blevins, All rights are reserved.
Return to
NeilBlevins.com














